Abstract
Biocomplexity views landscapes as complex systems, consisting of interactions of human and natural processes, in which landscape patterns are important emergent properties of complex dynamics. Spatially-explicit modeling approaches such as Cellular Automata (CA) and Agent Based Models (ABMs) are highly suited to the study of landscape dynamics and how landscape patterns form and evolve through interactions with heterogeneous places, environments, and actors. These models allow us to develop candidate explanations for specific landscape patterns, spatially simulate landscape patterns, examine likely future scenarios of change, and examine endogenous factors and exogenous shocks that can alter trajectories of landscape change resulting in possible shifts in the composition and spatial structure of the landscape.
Introduction
A complex system is one in which its multiple components interact in ways that link patterns and processes across scales. Further, complex systems focus on irreducible complexity arising from simplicity. This view sees the complex nature of systems as emerging from non-linearities due to large numbers of interactions involving feedbacks occurring at one or more lower levels within the system. Complexity theory holds that systems cannot be suitably understood without a focus on the feedbacks and nonlinearities that lead to emergent multi-scale phenomena. A complexity theory analysis aims at understanding feedback mechanisms and changes in state-space through nonlinearities and thresholds, in relation to a dynamic environment with the goal of understanding how simple, fundamental processes combine to produce complex holistic systems. Endogenous and exogenous factors combine in complex ways to alter the vulnerability and resilience of system components. Complex systems not only evolve through time, their past is co-responsible for its present behavior. Biocomplexity encompasses the complex interactions within and among ecological systems, the physical systems on which they depend, and the human systems with which they interact. Biocomplexity is the interdisciplinary and integrated study of coupled human-natural systems, often approached from the perspective of land use/land cover (LULC) change, to address the causes and consequences of landscape dynamics.
Our research is generally motivated by questions that seek understanding in broad areas of biocomplexity concern:
- How does a complex approach help explore the internal mechanisms of systems and provide plausible explanations?
- How do results derived from applying complexity theory help in understanding decision-making across levels of social organization ranging from individual households to national governments?
- How do fundamental characteristics of complex dynamics of coupled human-natural systems and the limits of predictability pertain to sustainable development?
- Do positive and negative feedbacks, and feedback switches, produce a system with a critical point subject to small or large effects of exogenous factors functioning through space and time lags?
- How can non-equilibrium systems, with feedbacks leading to nonlinearity, evolve into systems that exhibit criticality and capture key dynamics of LULC?
- How do space and time affect nonlinearities — do location, spatial properties, and space play important roles in complexity by allowing time lags to be scale dependent?
- What are the emergent patterns or trajectories of LULC change, are fractal characteristics evident, and do they organize around fronts of change and development?
Cellular Automata (CA)
CA models belong to a family of discrete, connectionist techniques used to investigate fundamental principles of dynamics, evolution, and self-organization. CA models are examples of mathematical systems constructed from many simple identical components that together are capable of complex behavior. CA approaches can be used to develop specific models for particular systems, and to abstract general principles applicable to a wide variety of complex systems. CA models do not describe a complex system with complex equations (e.g., differential equations, multilevel statistical modeling), but allow the complexity to emerge from interactions of basic building blocks of systems (e.g., individuals and households represented at the cell level) that follow simple rules.
The essential properties of a CA are: a regular n-dimensional lattice is where each cell of the lattice has a discrete state, and a dynamical behavior described through growth or transition rules. These rules describe the state of a cell for the next time step, depending upon the states of the cells in the defined spatial neighborhood. The essential components of a CA model are: (1) the cell — the basic element of a CA that is capable of storing defined states, (2) the lattice, or cells arranged in a spatial matrix, and (3) neighborhoods defined by growth or transition rules that perform changes to the state of the cells depending upon neighboring cells and their conditions. Four classes of behavior are recognized in CA models: fixed, periodic, chaotic, and complex.
Agent-Based Models
Agent based models examine the basic characteristics and activities of individual agents (e.g., individuals or households) as the basic building blocks. An agent based model may have multiple copies of the same type of agent, e.g. multiple copies of one type of plant or human actor, or multiple copies of multiple agents of different types, e.g. households, individuals, and government agencies. Agents differ in important characteristics. Their interactions may be dynamic, in that, the characteristics of the agents change over time as the agents adapt to their environment, learn from experiences through feedbacks, or “die” as they fail to alter behavior relative to new conditions and/or factors. The dynamics that describe how systems change are generally nonlinear, sometimes even chaotic, and seldom in any long-term equilibrium. Agents may be organized into groups of individuals or into nested hierarchies that may influence how the underlying system evolves over time. They are emergent and self-organizing in that macro-level behaviors emerge from the actions of individual agents as agents learn through experiences and change and develop feedbacks with finer scale building blocks.
In the context of understanding landscape change, i.e., LULC change, agents can include land owners, farmers, management agencies, and/or policy making bodies, all of whom make decisions or take actions that affect land-cover patterns and processes. By simulating the individual actions of many diverse actors, and measuring the resulting system behavior and outcomes over time (e.g., the changes in patterns of land cover), ABMs can be useful tools for studying the effects on processes that operate at multiple scales, organizational levels, and their effects.
ABMs have a number of strengths that contrast with traditional methods for modeling landscape change. In addition to the richer behavioral representations afforded by ABMs, because an ABM is a dynamical system, it can incorporate positive and negative feedbacks, such that the behavior of an agent has an influence on the subsequent behavior of other agents. These feedbacks can be used to represent the endogeneity of various driving forces of landscape change. By taking into account their commonalities and differences in structure, function, and evolution across time and space, ABMs and experimentation offer the possibility of considerable insights into system dynamics and behaviors. Agent based experiments provide flexibility and considerable analytical power to examine pattern and process relations, including policy issues.
Biocomplexity in Coupled Human-Natural Systems: Northern Ecuadorian Amazon
A complexity theory analysis of LULC change at frontier settings, using a CA approach, aims at understanding feedbacks and changes in state space through nonlinearities, and in relation to a dynamic and coupled human-natural system. As seen in frontier environments, LULC change patterns are not random, but self organized around development fronts that are shaped by geographic accessibility into the region and the constraints of resource endowments.
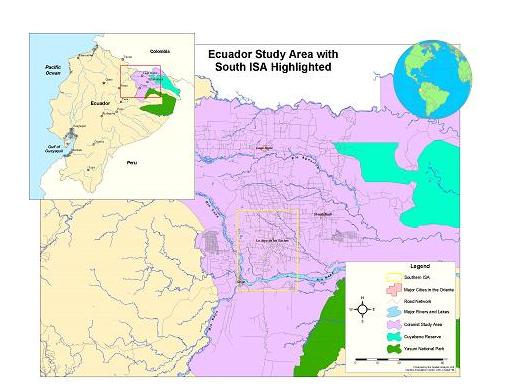
The tropical rainforest of northeastern Ecuador (Figure 1) is an area of complex interactions among a number of important and diverse stakeholders — (a) spontaneous colonists who have in-migrated from other regions of the country and settled on household farms; (b) newly emerging communities and market centers that have consolidated services, offer off-farm employment to colonists, and affect land use/land cover (LULC) through direct and indirect ways; (c) indigenous people who follow traditional practices, but are affected by the rise of commercial agriculture, oil production within their historical territories, and a transition to a consumer-based economy; (d) oil exploiters who have built roads and laid pipelines for petroleum extraction in colonist and indigenous areas; and (e) conservation and protected areas established by the government to impeded development and retain biodiversity in a rapidly transforming frontier environment. The greatest changes on the land are those created by agricultural colonists following in the wake of oil exploration, who gained access on roads that made isolated areas accessible for development. However, interactions among the groups and the regions that they’ve settled are complex, because feedbacks between spatial patterns and rates of change are known to occur at advancing fronts of settlement and land development that have implications for LULC patterns.
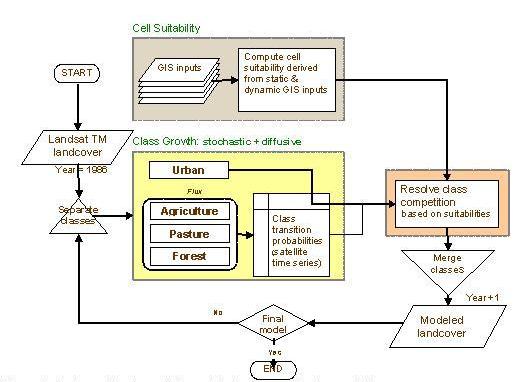
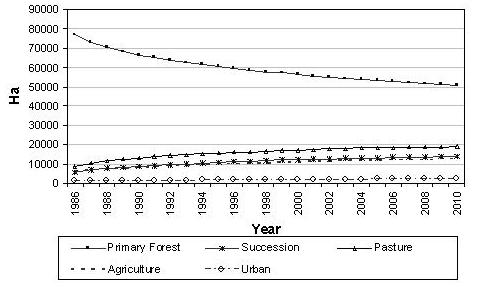
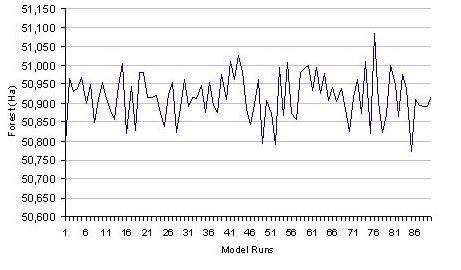
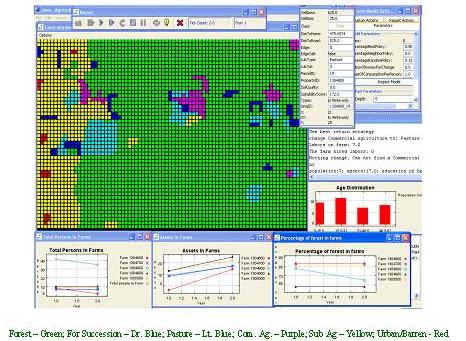
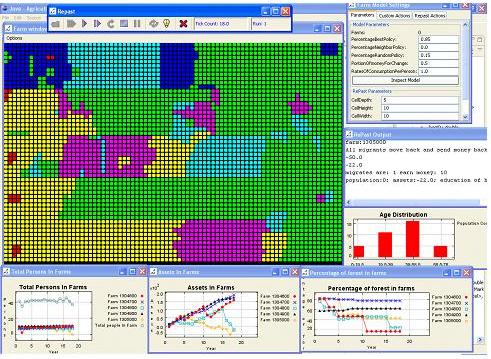
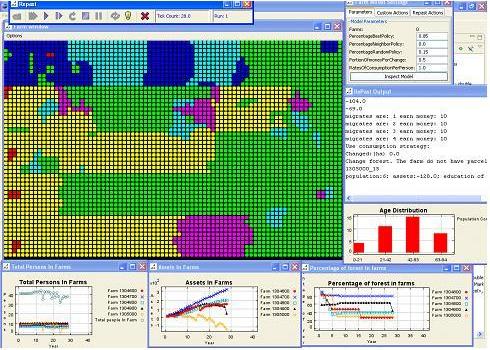
The preliminary simulations developed for the Northern Ecuadorian Amazon using CA have thus far suggested a more homogenous landscape with time, a scenario that fits the theoretical understanding of how in-migration of farmers into existing farms through resale, subdivision of farms to those engaged primarily in the burgeoning service sector, and the establishment of new development sectors alters the natural landscape through deforestation and agricultural extensification. In subsequent models, we are now including additional processes, for instance, that represent social (e.g., labor supply and off-farm employment), demographic (e.g., population density and household income), biophysical (e.g., terrain settings and site suitability for agriculture), and geographical (e.g., spatial linkages between farms and communities and geographic accessibility) factors (Figures 2 and 3). Figure 4 shows the variation in simulated land use/land cover through the period of the spatial simulation, and Figure 5 shows the variation of model outcomes as a consequence of stochastic processes in the CA model.
Agent Based Models
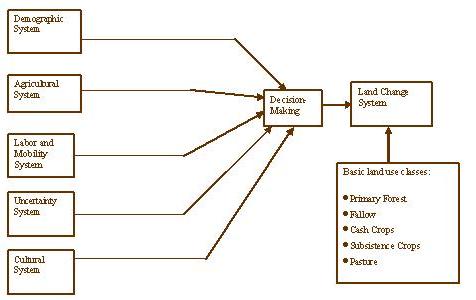
Our agent based model (ABM) recognizes autonomous decision-making entities (agents – households), an environment through which agents interact, rules that define the relationship between agents and their environment, and rules defining the sequence of actions in the model. Complex adaptive systems are self-organized systems that combine local processes to produce holistic systems. Macro-level behaviors “emerge” from the actions of individual agents as they learn through experiences and change and develop feedbacks with finer scale building blocks as agents. Our modeling approach integrates five sub-systems: demographic system, agricultural systems, labor and mobility system, cultural system, and uncertainty system (Figure 6). We are guided by the Multi-Phasic Response Theory in which land use/land cover change is the spatially-explicit response of a set of household adaptations to the changing socio-economic conditions and environmental factors. In addition, the Household Life Cycle is used to assess the stages of needs and development at the household level including (1) young parents who recently arrived in the area initiate forest clearings for subsistence crops, (2) parents with growing children become engaged in the cultivation of cash crops and pasture, (3) older parents with teenage children are related to a decrease in the cultivation of annuals and an increase in cattle raising and secondary vegetation, (4) pasture and perennial crops dominate with increasing proportions of secondary forest as parents age and children reach young adulthood, and (5) children begin to leave the household or subdivide the farm. We have generated the model using Re-Past software and JAVA programming. Figures 7-9 are Re-Past screen captures for years 2, 18, and 28 of the spatial simulation. The model is designed to examine household decision-making and land use/land cover dynamics.